Question

A platinum resistance thermometer has a resistance of 11.50 ohms at 0 oC and 17.35 ohms at 100 oC. Assuming that the resistance changes uniformly with temperature, what is the temperature when the resistance is 13.50 ohms?

Answer 1

`34.2^(\circ)C`

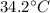
Step-by-step explanation:

The resistance increases linearly with the temperature - so we can write:

`\Delta R = k \Delta T`

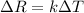
where

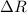`\Delta R` is the change in resistance

k is the coefficient of proportionality

`\Delta T` is the variation of temperature

In the first part of the problem, we have

`\Delta R = 17.35 - 11.50 =5.85\Omega`

`\Delta T = 100 -0 = 100^(\circ)C`

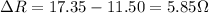
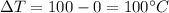
So the coefficient of proportionality is

`k=(\Delta R)/(\Delta T)=(5.85)/(100)=0.0585 \Omega ^(\circ)C^(-1)`

When the resistance is
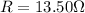`R=13.50\Omega`, the change in resistance with respect to the resistance at zero degrees is

`\Delta R' = 13.50-11.50 = 2.00 \Omega`

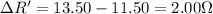
So we can find the change in temperature as:

`\Delta T' = (\Delta R)/(k)=(2.00)/(0.0585)=34.2^(\circ)`

So the new temperature is

`T_f = T_0 + \Delta T' = 0+34.2 = 34.2^(\circ)C`