Question

Find the area of a triangle bounded by the y-axis, the line f(x)=9−4/7x, and the line perpendicular to f(x) that passes through the origin.

Area =

Answer 1

The area of the triangle bounded by the y-axis is
`(7938)/(4225) √(65) \text { unit }^(2)`

SOLUTION:

Given,
`f(x)=9-(-4)/(7) x`

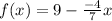
Consider f(x) = y. Hence we get

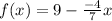`f(x)=9-(-4)/(7) x` --- eqn 1

`y=9-(4)/(7) x`

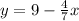
On rewriting the terms we get

4x + 7y – 63 = 0

As the triangle is bounded by two perpendicular lines, it is an right angle triangle with y-axis as hypotenuse.

Area of right angle triangle =
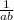`(1)/(ab)` where a, b are lengths of sides other than hypotenuse.

So, we need find length of f(x) and its perpendicular line.

First let us find perpendicular line equation.

Slope of f(x) =
`\frac{-x \text { coefficient }}{y \text { coefficient }}=(-4)/(7)`

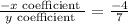
So, slope of perpendicular line =
`\frac{-1}{\text {slope of } f(x)}=(7)/(4)`

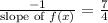
Perpendicular line is passing through origin(0,0).So by using point slope formula,

`y-y_(1)=m\left(x-x_(1)\right)`

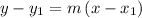
Where m is the slope and
`\left(\mathrm{x}_(1), \mathrm{y}_(1)\right)`

`y-0=(7)/(4)(x-0)`

`y=(7)/(4) x` --- eqn 2

4y = 7x

7x – 4y = 0

now, let us find the vertices of triangle, one of them is origin, second one is point of intersection of y-axis and f(x)

for points on y-axis x will be zero, to get y value, put x =0 int f(x)

0 + 7y – 63 = 0

7y = 63

y = 9

Hence, the point of intersection is (0, 9)

Third vertex is point of intersection of f(x) and its perpendicular line.

So, solve (1) and (2)

`\begin{array}{l}{9-(4)/(7) x=(7)/(4) x} \\\\ {9 * 4-(4 * 4)/(7) x=7 x} \\\\ {36 * 7-16 x=7 * 7 x} \\\\ {252-16 x=49 x} \\\\ {49 x+16 x=252} \\\\ {65 x=252} \\\\ {x=(252)/(65)}\end{array}`

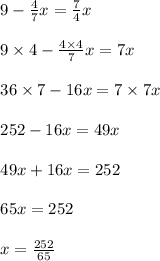
Put x value in (2)

`\begin{array}{l}{y=(7)/(4) * (252)/(65)} \\\\ {y=(441)/(65)}\end{array}`

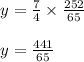
So, the point of intersection is
`\left((252)/(65), (441)/(65)\right)`

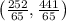
Length of f(x) is distance between
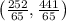`\left((252)/(65), (441)/(65)\right)` and (0,9)

`\begin{aligned} \text { Length } &=\sqrt{\left(0-(252)/(65)\right)^(2)+\left(9-(441)/(65)\right)^(2)} \\ &=\sqrt{\left((252)/(65)\right)^(2)+0} \\ &=(252)/(65) \end{aligned}`

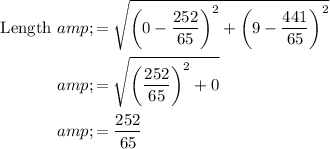
Now, length of perpendicular of f(x) is distance between
`\left((252)/(65), (441)/(65)\right) \text { and }(0,0)`

`\begin{aligned} \text { Length } &=\sqrt{\left(0-(252)/(65)\right)^(2)+\left(0-(441)/(65)\right)^(2)} \\ &=\sqrt{\left((252)/(65)\right)^(2)+\left((441)/(65)\right)^(2)} \\ &=\frac{\sqrt{(12 * 21)^(2)+(21 * 21)^(2)}}{65} \\ &=(63)/(65) √(65) \end{aligned}`

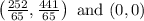
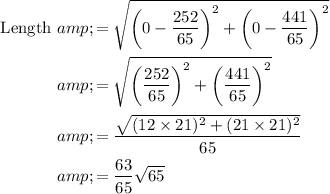
Now, area of right angle triangle =
`(1)/(2) * (252)/(65) * (63)/(65) √(65)`

`=(7938)/(4225) √(65) \text { unit }^(2)`

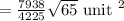
Hence, the area of the triangle is
`(7938)/(4225) √(65) \text { unit }^(2)`