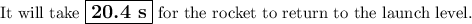Question

If you launch a bottle rocket into the sky with initial velocity 100m/s, how long will it take to come back to the launch height? Ignore wind /air resistance

Answer 1

`\large \boxed{\text{20.4 s}}`

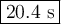
Step-by-step explanation:

I assume the rocket is going straight up. Then we need to deal only with the vertical direction.

Start with the equation

`v = v_(0) + at`

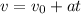
At t = 0, v₀ = 100 m/s.

At time t, at the height of the trajectory, v = 0.

a = g = -9.807 m·s⁻²

`\begin{array}{rcl}0 & = & 100 - 9.807t \\-100& = &-9.807t\\t & = & (100)/(9.807)\\\\& = & \text{10.20 s}\\\end{array}`

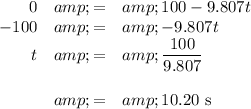
This is the time it takes to reach maximum height.

It will take the same time to reach the ground.

Thus,

Time of flight = 2t = 2 × 10.20 s = 20.4 s

`\text{It will take $\large \boxed{\textbf{20.4 s}}$ for the rocket to return to the launch level.}`