Answer:
Option B and C
Explanation:
We are given that
1.
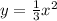
Differentiate w.r.t x
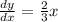
By using the formula
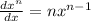
Rate of change of function depend on x. Hence, it is not constant.
2.
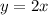
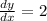
The rate of change of the function does not vary wit x.
Hence, it stays the same.
3.
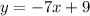
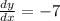
The rate of change of the function does not vary wit x.
Hence, it stays the same.
4.
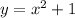
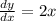
Rate of change of function depend on x. Hence, it is not constant.