Question

Which of the following functions functions has a rate of change that stays the same?

y=1/3x^2
y=2x
y=-7x+9
y=x^2+1

Answer 1

Option B and C

Explanation:

We are given that

1.
`y=(1)/(3)x^2`

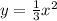
Differentiate w.r.t x

`(dy)/(dx)=(2)/(3)x`

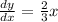
By using the formula

`(dx^n)/(dx)=nx^(n-1)`

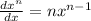
Rate of change of function depend on x. Hence, it is not constant.

2.
`y=2x`

`(dy)/(dx)=2`

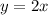
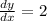
The rate of change of the function does not vary wit x.

Hence, it stays the same.

3.
`y=-7x+9`

`(dy)/(dx)=-7`

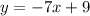
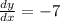
The rate of change of the function does not vary wit x.

Hence, it stays the same.

4.
`y=x^2+1`

`(dy)/(dx)=2x`

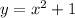
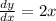
Rate of change of function depend on x. Hence, it is not constant.

Answer 2

y = 2x and y = -7x +9

Explanation:

The two "linear" functions are those that have a constant rate of change. Actually, the slope (inclination) they show when plotted is that "rate of change".

The function : y = 2x, has a constant positive rate given by its slope (2).

The function : y= -7x +9 has a constant negative rate given by its slope (-7)

The other two functions are quadratic, represented by parabolas, and therefore don't have a constant rate of change.