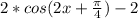Question

Write an equation of the cosine function with the given amplitude, period, phase shift, and vertical shift. amplitude: 2, period = π, phase shift = (–1/8)π , vertical shift = –2

Answer 1

`2*cos(2x+(\pi)/(4) )-2`

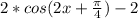
Explanation:

Recall the trigonometric definitions for the geometrical characteristics given to you:

For a General Harmonic function of the type:
`f(x)=A* cos(Bx+C)+D`

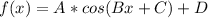
we define:

|A| = Amplitude of the function

Period of the function =
`(2\pi )/(B)`

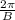
Phase shift =
`-(C)/(B)`

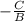
vertical shift = D

Therefore we can construct a function that includes the appropriate geometric characteristics requested by using:

A = 2

To find B we use the definition of period, and what value we want it to have:
`(2\pi )/(B)=\pi \\(2\pi )/(\pi)=B\\B=2`

To find C we use the definition of phase shift and the value we want it to have (also using the value for B we found in the step above):
`-(C)/(B)=-(\pi)/(8) \\-(C)/(2)=-(\pi)/(8)\\C=(2* \pi)/(8) =(\pi )/(4)`

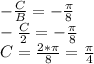
and finally, D = -2

Therefore the function will look like:
`2*cos(2x+(\pi)/(4) )-2`