Question

Given that f(x) = -x-2 and g(x)=x^2 find (f+g)(6)

Answer 1

The value of (f + g)(6) = 28

SOLUTION:

Given that f(x) = -x-2 and g(x) =
`x^(2)`

We need to find the value of (f+g)(6)

(f + g)(x) is an arithmetic combination of f(x) and g(x)

As, the operator between f and g is addition operator, the value of arithmetic combination becomes

(f + g)(x) = f(x) + g(x)

`\begin{array}{l}{=-X-2+X^(2)} \\ {=X^(2)-X-2}\end{array}`

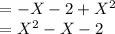
Now, put x = 6 in (f + g)(x)

(f + g)(6) =
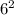`6^(2)` – 6 – 2

= 36 – 6 – 2

= 36 – 8 = 28

Hence, the value of (f + g)(6) = 28