Question

Twenty identical looking packets of white power are such that 15 contain cocaine and 5 do not. Four packets were randomly selected, and the contents were tested and found to contain cocaine. Two additional packets were selected from the remainder and sold by undercover police officers to a single buyer. What is the probability that the 6 packets randomly selected are such that the first 4 all contain cocaine and the 2 sold to the buyer do not?

Answer 1

The probability of selecting randomly 6 packets such that the first 4 contain cocaine and 2 not is 0.3522.

Explanation:

Probabilities of selecting 4 packets with the ilegal substance:

`((15)/(4))\\`=
`(15!)/(4!(15-4)!)`

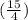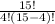
Combinassions possible= 1365

Probabilities of selecting 2 packets with white powder:

`((5)/(2))`=
`(5!)/(2!(5-2)!)`

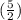Combinations possible= 10

Probabilities of selecting 6 packets from the totality of them:

`((20)/(6))` =
`(20!)/(6!(20-6)!)`

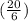Combinations possible= 38760

The probability of picking 4 with the substance and 2 with only white powder is:

`((15ncr4)(5ncr2))/((20ncr6))` = 0.3522

I hope this answer helps you.