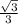Question

Simplify each expression as much as possible, and rationalize denominators when applicable. √((1/3)=?

Answer 1

`(√(3))/(3)`

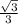
Explanation:

So we start with the original expression to be:

`\sqrt{(1)/(3)}`

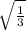
so we need to first split the square root into two, one for the numerator and another one for the denominator so we get:

`(√(1))/(√(3))`

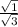
we can now simplify that so we get:

`(1)/(√(3))`

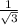
we can now rationalize the denominator by multiplying the fraction by
`(√(3))/(√(3))`

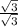
so we get:

`(1)/(√(3))*(√(3))/(√(3))`

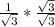
we do the multiplication so we end up with:

`(√(3))/((√(3))^(2))`

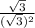
which simplifies to:

`(√(3))/(3)`