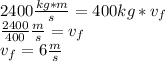Question

Sayid made a chart listing data of two colliding objects. A 5-column table titled Collision: Two Objects Stick Together with 2 rows in the first 3 columns and 1 row in the last 2 columns. The first column labeled Object has entries X, Y. The second column labeled Mass before Collision (kilograms) has entries 300, 100. The third column labeled Velocity before Collision (meters per second) has entries 10, negative 6. The fourth column labeled Mass after Collision (kilograms) has entry 400. The fifth column labeled Velocity after Collision (meters per second) has entry ?. According to the law of conservation of momentum, what is the missing value in the chart? 4 6 10 16

Answer 1

B

Step-by-step explanation:

Answer 2

6 m/s is the missing final velocity

Step-by-step explanation:

From the data table we extract that there were two objects (X and Y) that underwent an inelastic collision, moving together after the collision as a new object with mass equal the addition of the two original masses, and a new velocity which is the unknown in the problem).

Object X had a mass of 300 kg, while object Y had a mass of 100 kg.

Object's X initial velocity was positive (let's imagine it on a horizontal axis pointing to the right) of 10 m/s. Object Y had a negative velocity (imagine it as pointing to the left on the horizontal axis) of -6 m/s.

We can solve for the unknown, using conservation of momentum in the collision: Initial total momentum = Final total momentum (where momentum is defined as the product of the mass of the object times its velocity.

In numbers, and calling
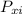`P_(xi)` the initial momentum of object X and
`P_(yi)` the initial momentum of object Y, we can derive the total initial momentum of the system:
`P_(total)_i=P_(xi)+P_(yi)= 300*10 (kg*m)/(s) -100*6(kg*m)/(s) =\\=(3000-600 )(kg*m)/(s) =2400 (kg*m)/(s)`

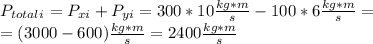
Since in the collision there is conservation of the total momentum, this initial quantity should equal the quantity for the final mometum of the stack together system (that has a total mass of 400 kg):

Final momentum of the system:
`M * v_f=400kg * v_f`

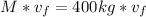
We then set the equality of the momenta (total initial equals final) and proceed to solve the equation for the unknown(final velocity of the system):

`2400 (kg*m)/(s) =400kg*v_f\\(2400)/(400) (m)/(s) =v_f\\v_f=6 (m)/(s)`