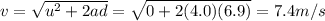Question

A 2.0 kg wood block is launched up a wooden ramp that is inclinedat a 35* angle. The block’s initial speed is 10m/s. (Giventhat μk = 0.20)

a. What vertical height does the block reach above its startingpoint?
b. What speed does it have when it slides back down to its startingpoint?

Answer 1

a) 4.0 m

We can solve this part by writing the equations of motion along the two directions: perpendicular to the slope and parallel to the slope.

Perpendicular to the slope:

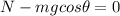`N-mgcos \theta =0` (1)

where N is the normal reaction, m = 2.0 kg is the mass of the block, g = 9.8 m/s^2 is the acceleration of gravity,
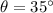`\theta=35^(\circ)` is the angle.

Parallel to the slope:

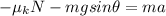`-\mu_k N -mgsin \theta = ma` (2)

where
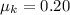`\mu_k=0.20` is the coefficient of friction, and a the acceleration, and where we have chosen up the slope as positive direction, so both forces are negative.

From (1) we get

`N=mg cos \theta`

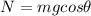
And substituting into (2), we can find the acceleration:

`-\mu_k mg cos \theta -mgsin \theta = ma\\a=-\mu_k g cos\theta - g sin \theta = -(0.20)(9.8)(cos 35^(\circ))-(9.8)(sin 35^(\circ))=-7.2 m/s^2`

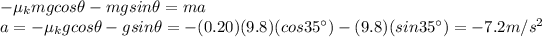
where the negative sign means the direction is down the slope.

Now we can find the distance travelled along the slope by using the SUVAT equation

`v^2-u^2=2ad`

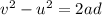
where

v = 0 is the velocity when the block comes to rest

u = 10 m/s is the initial velocity

d is the distance travelled along the slope

Solving for d,

`d=(v^2-u^2)/(2a)=(0-(10)^2)/(2(-7.2))=6.9 m`

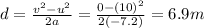
And so, the vertical heigth gained by the block is

`h=d sin \theta = (6.9)(sin 35^(\circ))=4.0 m`

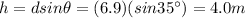
b) 7.4 m/s

The equation of motion along the direction parallel to the slope in this case is

`-\mu_k N +mgsin \theta = ma`

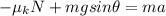
where this time we have taken down the slope as positive direction, so the component of the weight is positive while the frictional force is negative since the block slides downward (while friction acts upward). Solving for a, we find the new acceleration:

`a=-\mu_k g cos \theta + g sin \theta = -(0.20)(9.8)(cos 35^(\circ))+(9.8)(sin 35^(\circ))=4.0 m/s^2`

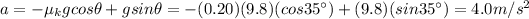
Now we can use again the SUVAT equation

`v^2-u^2=2ad`

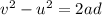
where

v is the final velocity

u = 0 is the initial velocity

d = 6.9 m is the distance travelled along the slope

a = 4.0 m/s^2 is the acceleration

Solving for v,

`v=√(u^2+2ad)=√(0+2(4.0)(6.9))=7.4 m/s`