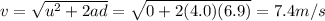a) 4.0 m
We can solve this part by writing the equations of motion along the two directions: perpendicular to the slope and parallel to the slope.
Perpendicular to the slope:
 (1)
(1)
where N is the normal reaction, m = 2.0 kg is the mass of the block, g = 9.8 m/s^2 is the acceleration of gravity,
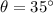 is the angle.
is the angle.
Parallel to the slope:
 (2)
(2)
where
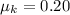 is the coefficient of friction, and a the acceleration, and where we have chosen up the slope as positive direction, so both forces are negative.
is the coefficient of friction, and a the acceleration, and where we have chosen up the slope as positive direction, so both forces are negative.
From (1) we get
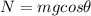
And substituting into (2), we can find the acceleration:

where the negative sign means the direction is down the slope.
Now we can find the distance travelled along the slope by using the SUVAT equation
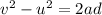
where
v = 0 is the velocity when the block comes to rest
u = 10 m/s is the initial velocity
d is the distance travelled along the slope
Solving for d,

And so, the vertical heigth gained by the block is
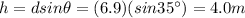
b) 7.4 m/s
The equation of motion along the direction parallel to the slope in this case is
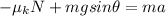
where this time we have taken down the slope as positive direction, so the component of the weight is positive while the frictional force is negative since the block slides downward (while friction acts upward). Solving for a, we find the new acceleration:

Now we can use again the SUVAT equation
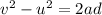
where
v is the final velocity
u = 0 is the initial velocity
d = 6.9 m is the distance travelled along the slope
a = 4.0 m/s^2 is the acceleration
Solving for v,