To check if a piecewise defined function is continuous, you need to check how the pieces "glue" together when you step from one domain to the other.
So, the question is: what happens at x=3? If you reach x=3 from values slightly smaller than 3, you obey the rule f(x)=log(3x). So, as you approach 3, you get values closer and closer to
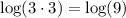
Similarly, if you reach x=3 from values slightly greater than 3, you obey the rule f(x)=(4-x)log(9). So, as you approach 3, you get values closer and closer to
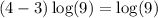
So, the function is continuous at x=3, because both pieces approach log(9) as x approaches 3.