Option C
Answer:
According to the general equation for conditional probability, If
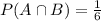 and P(B) =
and P(B) =
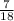 then
then
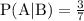
Solution:
Given that
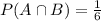 and
and
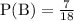
We have to find the value of
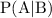
We know that
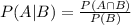
In order to find the value of
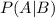 substitute the value
substitute the value
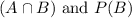 from the given data.
from the given data.
Step 1:
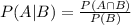
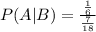
Step 2:
By evaluating the above term we get below expression
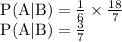
Hence we found the value for
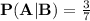 using the given data.
using the given data.