Question

According to the general equation for conditional probability, if P(A n B) = 1/6 and P(B) = 7/18 what is P ( A|B)?

a. 2/7
b. 5/7
c. 3/7
d. 4/7

Answer 1

Option C

Answer:

According to the general equation for conditional probability, If
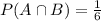`P(A \cap B)=(1)/(6)` and P(B) =
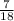`(7)/(18)` then
`\mathrm{P}(\mathrm{A} | \mathrm{B})=(3)/(7)`

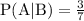
Solution:

Given that
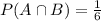`P(A \cap B)=(1)/(6)` and
`\mathrm{P}(\mathrm{B})=(7)/(18)`

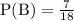
We have to find the value of
`\mathrm{P}(\mathrm{A} | \mathrm{B})`

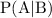
We know that
`P(A | B)=(P(A \cap B))/(P(B))`

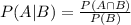
In order to find the value of
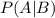`P(A | B)` substitute the value
`(A \cap B) \text { and } P(B)` from the given data.

Step 1:

`P(A | B)=(P(A \cap B))/(P(B))`

`P(A | B)=((1)/(6))/((7)/(18))`

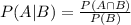
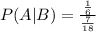
Step 2:

By evaluating the above term we get below expression

`\begin{array}{l}{\mathrm{P}(\mathrm{A} | \mathrm{B})=(1)/(6) * (18)/(7)} \\ {\mathrm{P}(\mathrm{A} | \mathrm{B})=(3)/(7)}\end{array}`

Hence we found the value for
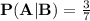`\mathbf{P}(\mathbf{A} | \mathbf{B})=(3)/(7)` using the given data.