Question

A weighted, frictionless piston-cylinder device initially contains 5.25 kg of R134a as saturated vapor at 500 kPa. The container loses heat to the surroundings during an isobaric process, the energy lost is 976.71 kJ. (a) Determine the change in entropy (kJ/K) of the R134a during this process. (b) Show the process on a T-s diagram

Answer 1

-6.326 KJ/K

Step-by-step explanation:

A) the entropy change is defined as:

`delta S_(12)=\int\limits^2_1  \, (dQ)/(T)`

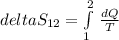
In an isobaric process heat (Q) is defined as:

`Q= m*Cp*dT`

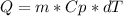
Replacing in the equation for entropy

`delta S_(12)=\int\limits^2_1 (m*Cp*dT)/(T)`

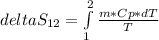
m is the mass and Cp is the specific heat of R134a. We can considerer these values as constants so the expression for entropy would be:

`delta S_(12)= m*Cp*\int\limits^2_1 ( dT )/(T)`

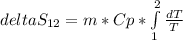
Solving the integral we get the expression to estimate the entropy change in the system

`delta S_(12)= m*Cp *ln((T_(2))/(T_(1)))`

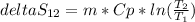
The mass is 5.25 Kg and Cp for R134a vapor can be consulted in tables, this value is
`0.85(kJ)/(Kg*K)`

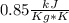
We can get the temperature at the beginning knowing that is saturated vapor at 500 KPa. Consulting the thermodynamic tables, we get that temperature of saturation at this pressure is: 288.86 K

The temperature in the final state we can get it from the heat expression, since we know how much heat was lost in the process (-976.71 kJ). By convention when heat is released by the system a negative sign is used to express it.

`Q= m*Cp*dT`

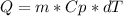
With
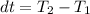`dt=T_(2)-T_(1)` clearing for T2 we get:

`T_(2)=(Q)/(m*Cp)+T1= (-976.71kJ)/(5.25Kg*0.85(kJ)/(Kg*K))+288.86 K =69.98 K`

Now we can estimate the entropy change in the system

`delta S_(12)= m*Cp*ln((T_(2))/(T_(1)))= 5.25Kg*0.85(kJ)/(Kg*K)*ln((69.98)/(288.861))= -6.326(kJ)/(K)`

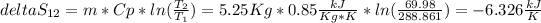
The entropy change in the system is negative because we are going from a state with a lot of disorder (high temperature) to one more organize (less temperature. This was done increasing the entropy of the surroundings.

b) see picture.