Answer:
initial quality = 0.3690
heat transfer = 979.63 kJ/kg
Step-by-step explanation:
Given data:
volume of tank 0.45^3
weight of water 12 kg
Initial pressure 20 bar
final pressure 4 bar
Specific volume
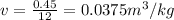
At Pressure = 20 bar, from saturated water table
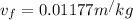
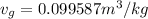
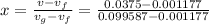
inital quality is x =0.3690
Heat transfer is calculated as
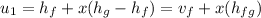
from saturated water table, for pressure 20 bar ,
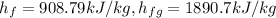
=908.79 + 0.0357(1890.7)
= 979.63 kJ/kg