Answer:
The force induced on the aircraft is 2.60 N
Solution:
As per the question:
Power transmitted,
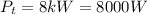
Now, the force, F is given by:
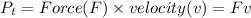 (1)
(1)
where
v = velocity
Now,
For a geo-stationary satellite, the centripetal force,
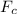 is provided by the gravitational force,
is provided by the gravitational force,
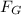 :
:
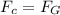
![(mv^(2))/(R) = \frac{GM_(e)m{R^(2)}]()
Thus from the above, velocity comes out to be:
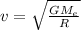
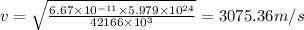
where
R =
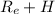
R =
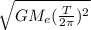
where
G = Gravitational constant
T = Time period of rotation of Earth
R is calculated as 42166 km
Now, from eqn (1):
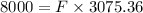
F = 2.60 N