Answer:
There are 2 expected readings greater than 2.70 V
Solution:
As per the question:
Total no. of readings, n = 60 V
Mean of the voltage,
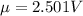
standard deviation,
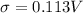
Now, to find the no. of readings greater than 2.70 V, we find:
The probability of the readings less than 2.70 V,
 :
:
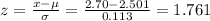
Now, from the Probability table of standard normal distribution:
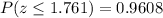
Now,

Now, for the expected no. of readings greater than 2.70 V:
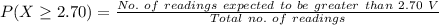
No. of readings expected to be greater than 2.70 V =
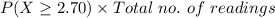
No. of readings expected to be greater than 2.70 V =
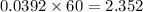 ≈ 2
≈ 2