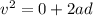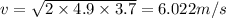Answer:
The maximum speed is 6.022 m/s
Solution:
As per the question:
Distance covered by the elevator in the upward direction, d = 3.7 m
Maximum force exerted by the elevator on the passenger = 1.59 w N
where
w = weight of the passenger = mg
where
m = mass of the passenger
g = acceleration due to gravity =

Therefore,
Maximum force exerted by the elevator on the passenger = 1.59mg N
Now, for the maximum speed of the elevator:
Net force on the floor of the elevator when it moves upwards:
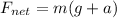
Thus
For maximum acceleration:
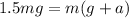
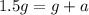
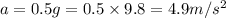
Now, from the third eqn of motion with initial velocity 0: