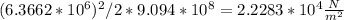Question

A 10 cm long bar, measuring 1 cm in diameter is loaded under tension. Assuming yield occurs at a load of 500 N, which corresponds to a 0.7% elongation, determine the modulus of resilience of this bar.

Answer 1

`2.23*10^(4)(N)/(m^(2) )`

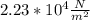
Step-by-step explanation:

Modulus of resilience is the maximum amount of strain that an elastic material can support per unit volume, without deformation, and is calculated using the following equation:

μ = σ^2 ÷ 2*E

σ = yield strain= force / cross area

force = 500N; area=π*
`r^(2)`=
`{7.8540^(-5)m^(2)`

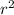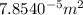
σ =
`(500N)/(7.8540^(-5)m^(2) ) =6.3662*10^(6) (N)/(m^(2) )`

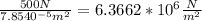
E= young modulus: relation between stress and strain, measures stiffness

E=σ/∈, where

∈=(L-Lo)/Lo=7*
`10^(-3)`

where

L=current length = 10 cm * 1.007 = 1.0070*
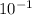`10^(-1)` m

Lo=original lenght = 10 cm = 1.0*
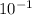`10^(-1)`m

so, E=σ/∈ =
`9.0094*10^(8)`

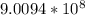
μ = modulus of resilience =
`({6.3662*10^(6)})^(2) / 2*9.094*10^(8) = 2.2283*10^(4) (N)/(m^(2) )`