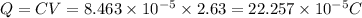Answer:
Charge stored after insertion will be

Step-by-step explanation:
We have given potential difference V =2.63 V
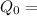 charge stored by the capacitor when without dielectric =
charge stored by the capacitor when without dielectric =
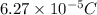
We know that
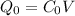 , here
, here
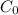 is capacitance without dielectric
is capacitance without dielectric
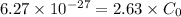
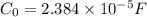
We have given
k = dielectric constant = 5.99
C = Capacitance with the dielectric = k
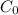 = 3.55×
= 3.55×
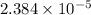 =
=
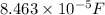
Potential difference is due to the external charging source so it remains same
V = potential difference after insertion = 2.63 volts
New charge stored ,