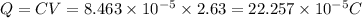Question

An initially uncharged air-filled capacitor is connected to a 2.63 V charging source. As a result, 6.27×10−5 C of charge is transferred from one of the capacitor's plates to the other. Then, while the capacitor remains connected to the charging source, a sheet of dielectric material is inserted between its plates, completely filling the space. The dielectric constant ????κ of this substance is 3.55. Find the capacitor's potential difference and charge after the insertion.

Answer 1

Charge stored after insertion will be
`22.257* 10^(-5)C`

Step-by-step explanation:

We have given potential difference V =2.63 V

`Q_0=` charge stored by the capacitor when without dielectric =
`6.27* 10^(-5)C`

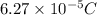
We know that
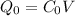`Q_0=C_0V`, here
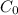`C_0` is capacitance without dielectric

`6.27* 10^(-27)=2.63* C_0`

`C_0=2.384* 10^(-5)F`

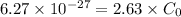
We have given

k = dielectric constant = 5.99

C = Capacitance with the dielectric = k
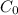`C_0` = 3.55×
`2.384* 10^(-5)` =
`8.463* 10^(-5)F`

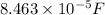
Potential difference is due to the external charging source so it remains same

V = potential difference after insertion = 2.63 volts

New charge stored ,
`Q=CV=8.463* 10^(-5)* 2.63=22.257* 10^(-5)C`