Question

A sheet metal part that is 5.0 mm thick, 85 mm long, and 20 mm wide is bent in a wiping die to an included angle of 90 degrees and a bend radius of 7.5 mm. The bend is in the middle of the 85 mm length, so that the bend axis is 20 mm long. The metal has a yield strength of 220 MPa and a tensile strength of 340 MPa. Compute the force requires to bend the part, given the die opening of 8 mm.

Answer 1

force required to bend the part is 7012.5 N

Step-by-step explanation:

force required to bent can be calculated by using following relation
`F = (k(TS)wt^2)/(D)`

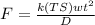
Where,

k is constant = 0.33 for wiping die

TS = tensile strength = 340\times 10^6

w = width of part = 20 mm = 0.020 m

t = thickness = 5.00 mm = 0.005 m

D = opening dimension of die = 8mm = 0.008 m

putting all value in the above formula

`F = (0.33* 340* 10^6* 20* 10^(-3)* (5 * 10^(-3))^2)/(8* 10^(-3))`

F = 7012.5 N

Therefore force required to bend the part is 7012.5 N

Answer 2

F=7.012 KN

Step-by-step explanation:

We know that force require for bending is

`F=K(\sigma_twt^2)/(D)`

Where

K=Constant

t=Thickness

D=Die opening

w=Width

`\sigma_t`=Tensile strength

Here K= 0.33

Now by putting the all given values

`F=K(\sigma_twt^2)/(D)`

`F=0.33* (340* 10^6* 0.02* (0.005)^2)/(0.008)`

F=7012.5 N

F=7.012 KN