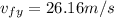Question

A projectile is fired horizontally from a gun that is 35.0 m above flat ground, emerging from the gun with a speed of 110 m/s. (a) How long does the projectile remain in the air? (b) At what horizontal distance from the firing point does it strike the ground? (c) What is the magnitude of the vertical component of its velocity as it strikes the ground?

Answer 1

(a) t = 2.67 s

(b) x= 293.7 m

(c)
`v_(fy) = 26.16 m/s`

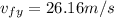
Step-by-step explanation:

Conceptual analysis:

Projectile movement is semi-parabolic,then, We aply the following formulas:

y = y₀+ v₀₁t + (1/2)*g*t² Formula 1

x= v₀ₓ * t Formula 2

vf₁= v₀₁+g*t Formula 3

Where

x: horizontal distance (m)

v₀ₓ : initial speed in x of the projectile (m/s)

y: final height of the projectile (m)

y₀ : initial height of the projectile (m)

v₀₁: initial speed in y of the projectile (m/s)

vf₁: final speed in y of the projectile (m/s)

g : acceleration due to gravity ( m/s²)

t : time (s)

Known data

y₀= -35 m

v₀ₓ = 110 m/s

v₀₁ = 0

g = 9.8 m/s²

t = time (s)

Problem development

We replace data in formula (1) to calculate the time that the projectile remains in the air, that is, when y = 0.

Because the projectile moves down the sign of the equation is positive in the term (1/2)*g*t²:

a)y = y₀+ v₀₁t + (1/2)*(g)*(t)²

0 = -35 +0+ (1/2) *(9.8) (t)²

35= 4.9 *(t)²

t² = 35/4.9

`t = \sqrt{(35)/(4.9) }`

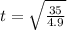
t = 2.67 s

b) We apply the formula 2 to calculate horizontal distance from the firing point does it strike the ground:

x= 110 m/s * 2.67 s

x= 293.7 m

c) Magnitude of the vertical component of its velocity as it strikes the ground

We replace data in Formula 3

vf₁= v₀₁+g*t

vf₁= 0+9.8*2.67 = 26.16 m/s

`v_(f1) = v_(fy)`

`v_(fy) = 26.16 m/s`