Question

Which statement is true about the coordinates of points A and B?

Answer 1

Option A)

`\displaystyle(y)/(x)\text{ of point B} = (y)/(x) \text{ of poinrt A}`

Explanation:

We are given the following in the question:

Point A and B lies on the line with the equation:

`y =\displaystyle(3)/(4)x`

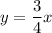
Let
`(x_1,y_1)` be the coordinates of A and let
`(x_2,y_2)` be the coordinates of point B, then, these points satisfy the equation of the given line.

Thus, we can write:

`y_1 =\displaystyle(3)/(4)x_1\\\\(y_1)/(x_1)=(3)/(4)`

\
`y_2 =\displaystyle(3)/(4)x_2\\\\(y_2)/(x_2)=(3)/(4)`

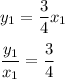
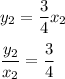
Thus, we can write,

`\displaystyle(y_1)/(x_1) = (y_2)/(x_2) = (3)/(4)`

Thus, from the given statements, the true statement is

`\displaystyle(y)/(x)\text{ of point B} = (y)/(x) \text{ of poinrt A}`

Answer 2

`(y)/(x)\text{ for point }A=(y)/(x)\text{ for point B }`

Explanation:

From the graph, you can see that both points A and B lie on the same straight line given by equation

`y=(3)/(4)x`

Now, if point with coordinates (x,y) lies on the line, then its coordinates satisfy the equation.

So, for point
`A(x_A,y_A):`

`(y_A)/(x_A)=(3)/(4)`

for point
`B(x_B,y_B):`

`(y_B)/(x_B)=(3)/(4)`

This means the first statement

`(y)/(x)\text{ for point }A=(y)/(x)\text{ for point B }`

is true