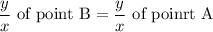Answer:
Option A)
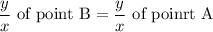
Explanation:
We are given the following in the question:
Point A and B lies on the line with the equation:
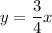
Let
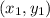 be the coordinates of A and let
be the coordinates of A and let
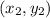 be the coordinates of point B, then, these points satisfy the equation of the given line.
be the coordinates of point B, then, these points satisfy the equation of the given line.
Thus, we can write:
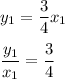
\
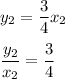
Thus, we can write,
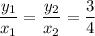
Thus, from the given statements, the true statement is