Question

Suppose that a random sample of size 25 is to be selected from a population with mean 41 and standard deviation 9. What is the approximate probability that X will be more than 0.5 away from the population mean? a) 0.7812b) 0.2188c) 0.4188d) 0.0443e) 0.4376f) None of the above

Answer 1

The probability that X will be more than 0.5 away fro the population

mean is 0.7812 ⇒ answer a

Explanation:

* Let us explain how to solve the problem

- The sample size n is 25

- The mean of the population μ is 41

- The standard deviation σ is 9

- We need to find the approximate probability that X will be more than

0.5 away from the population mean

∵ z-score = (X - μ)/(σ/√n)

∵ X - μ = 0.5

- That means X > 41 + 0.5, OR X < 41 - 0.5

- Then we need to find P(X > 41.5) and P(X < 40.5)

∵ z =
`(41.5-41)/((9)/(√(25)))` = 0.2778

∵ z =
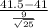`(40.5-41)/((9)/(√(25)))` = -0.2778

- Let us use the normal distribution table to find the corresponding

area to z-score

∵ P(z < 0.2778) = 0.6116

∵ P(z > -0.2778) = 0.3928

- P(40.5 < X < 41.5) = P( -0.2778 < z < 0.2778)

∴ The probability of X to be with in 0.5 = 0.6116 - 0.3928

∴ The probability of X to be with in 0.5 = 0.2188

∵ The probability of X to be more than 0.5 away from the population

mean = 1 - 0.2188

∴ P(X > 41.5) OR P(X < 40.5) = 0.7812

* The probability that X will be more than 0.5 away fro the population

mean is 0.7812