Answer:
After 2 seconds the object reach its maximum height of 80 feet.
Explanation:
Consider the provided function.
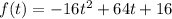
The function is a downward parabola.
The object will reach its max height at the vertex of the parabola.
The vertex of the parabola is given by
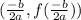 ,
,
Where the standard form is
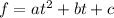 .
.
By comparing the provided function with the standard form.
a=-16, b=64 and c=16
Thus, the vertex are:
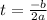
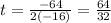
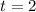
Now substitute the value of t in the provided function.
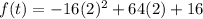
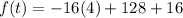
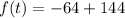
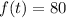
Hence, after 2 seconds the object reach its maximum height of 80 feet.