Question

o keep the calculations fairly simple, but still reasonable, we shall model a human leg that is 92.0cm long (measured from the hip joint) by assuming that the upper leg and the lower leg (which includes the foot) have equal lengths and that each of them is uniform. For a 70.0kg person, the mass of the upper leg would be 8.60kg , while that of the lower leg (including the foot) would be 5.30kg . Find the -coordinate of the center of mass of this leg, relative to the hip joint, if it is stretched out horizontally.

Answer 1

81.1 cm

Explanation:

The sum of moments about the hip joint is ...

(8.60 kg)(92 cm/2) + (5.30 kg)(92 cm +92 cm/2))

= 395.6 kg·cm +731.4 kg·cm = 1127 kg·cm

The mass of the leg is 8.60 +5.30 kg = 13.9 kg, so the above moment is equivalent to that mass at a distance of ...

(1127 kg·cm)/(13.9 kg) = 81.08 cm

The center of mass of the stretched-out leg is about 81.1 cm from the hip.

Answer 2

(40.5;0) cm

Explanation:

We know that:

The length of the leg is:
`l=92cm`

The problem says that each part of the leg has the same length, that is:

`l_(upper)=(92)/(2) = 46cm= l_(lower)`

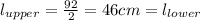
Also, the leg is uniform, so the center of mass of each part is in the middle, this is the position (r):

`r_(upper) = (46)/(2)= 23cm\\ r_(lower) = 46 + 23 = 69cm`

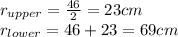
This means that the center of mass of the upper leg is 23cm from the hip, and the lower leg if 69c m from the hip.

In addition, we know each mass:

`m_(upper) = 8.60kg\\m_(lower)=5.30kg`

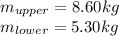
Now, we have all values needed, we use the proper equation to calculate the center of mass of the leg:

`r \ _(CM) = (m_(upper)r_(upper)  + m_(lower)r_(lower) )/(m_(upper)+m_(lower)) \\r \ _(CM) =((8.60)(23)+(5.30)(69))/(8.60+5.30) =(197.8+365.7)/(13.9) \\r \ _(CM) =40.5cm`

Therefore, the center of mass of the leg is 40.5m from the hip in a horizontal direction because it's stretched out horizontally Specifically, the coordinates are (40.5;0) cm.