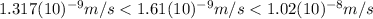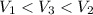Answer:

a)
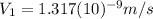
b)
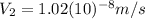
c)
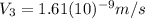
Explanation:
Assuming these objects are moving with uniform circular motion (and the orbit is perfectly circular), the velocity will be given by the following equation:
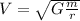
Where:
 is the velocity of the object, which is assumed as constant.
is the velocity of the object, which is assumed as constant.
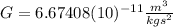 is the Gravitational Constant
is the Gravitational Constant
 is the mass of the object
is the mass of the object
 is the radius of the orbit
is the radius of the orbit
Knowing this, let's begin with the answers:
a. a 5-kg object orbiting Earth halfway to the moon
In this case the radius of the orbit is the half of the distance between the Earth and the moon:
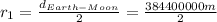
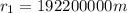
And the mass will be
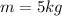 . So, the equation of the velocity is:
. So, the equation of the velocity is:
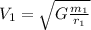
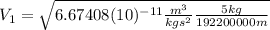
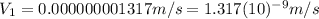 This is the velocity of the first object
This is the velocity of the first object
b. a 10-kg object orbiting Earth just above Earth's surface
Now the radius of the orbit is approximately the radius of the Earth:

And the mass is
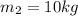 . So, the equation of the velocity is:
. So, the equation of the velocity is:
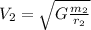
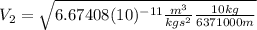
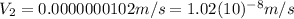 This is the velocity of the second object
This is the velocity of the second object
c. a 15-kg object orbiting Earth at the same distance as the Moon
With this last case, the radius of the orbit is equal to the distance between the Earth and the Moon:

And the mass is
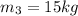 . So, the equation of the velocity is:
. So, the equation of the velocity is:
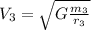

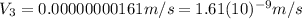 This is the velocity of the third object
This is the velocity of the third object
Finally, comparing the velocity of the three objects we have: