Question

You and your friend are in a canoe race. Your friend is a half mile in front of you and paddling 3 miles per hour. You are paddling 3.4 miles per hour. a. You are 8.5 miles from the finish line. How long will it take you to catch up to your friend? You will catch up to your friend after paddling for hour(s). b. You both maintain your paddling rates for the remainder of the race. How far ahead of your friend will you be when you cross the finish line? You will be mile(s) ahead of your friend when you finish the race.

Answer 1

It will take you 1.25 hours to catch up to your friend.

After you pass them, if they keep paddling at their current rate (3 miles) then you will be 0.5 miles ahead.

Answer 2

a. 1.25 hours

b. 0.5 miles ahead

Explanation:

This problem can be easily solved with the use of relative speed, then a problem of two bodies become a problem of one object.

The relative speed between two objects moving in the same direction is:

`v_(r)=|v_(a)-v_(b)|`

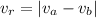
In the problem:

`v_(r)=|3mi/h-3.4mi/h|=0.4 mi/h\\`

What this relative speed means is the speed at which you are catching your friend up, then in order to catch your friend up you need to paddle the distance your friend is in front of you.

The time necesary to catch your friend up is:

`t=(distance)/(v_(r)) =(0.5miles)/(0.4(miles)/(h) ) =1.25 hours`

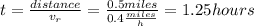
The distance that you paddle in order to cath your friend up is:

`d=vt=3.4(miles)/(h)(1.25h)=4.25 miles`

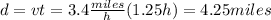
Then you are 4.25 miles from the finish line (8.5 miles - 4.25 miles) when you catch your friend up. The time necesary to cross the finish line is:

`t=(distance)/(v)=(4.25 miles)/(3.4 (miles)/(h) )=1.25 hours`

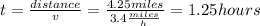
In that time, your friend will paddle:

`d=v_(friend)t=3(miles)/(h)1.25 h = 3.75 miles`

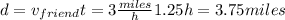
Then, when you cross the finish line you will be 0.5 miles ahead of your friend (4.25 miles - 3.75 miles).