Answer:
The correct answer is option B.
Step-by-step explanation:
Einstein mass energy relationship
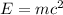
Given mass of star = M =
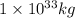
Mass of star used to make nuclear energy = m=0.1% of M
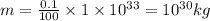
Speed of light = c =

Nuclear energy generated = E
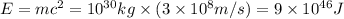
Solar power of the Star,P =
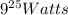
Total life time of the star = T



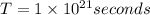
Total life time of the star is
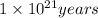 .
.