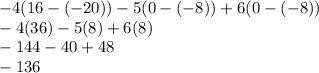Answer:
k = -6
w = ±9
f = -7
Determinant = -136
Explanation:
![\left[\begin{array}{cc}-12&-w^(2)\\2f&3\end{array}\right] =\left[\begin{array}{cc}2k&-81\\-14&3\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/owwapn4r7qtn7mtdlo0cj3g8yrjh5es8v3.png)
Each cell in the left matrix equals the corresponding cell in the right matrix:
-12 = 2k → k = -6
-w² = -81 → w = ±9
2f = -14 → f = -7
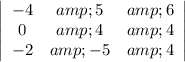
To find the determinant of a 3x3 matrix, you can use something called "Laplace expansion".
Start with the first column in the top row (-4). If you block out the row and column containing that cell, you get a 2x2 matrix:
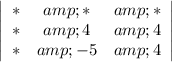
Multiply the -4 by the determinant of that 2x2 matrix:
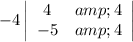
Repeat for the other two cells in the top row.
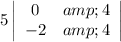
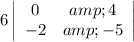
Add them together, alternating the signs (first column positive, second column negative, third column positive).
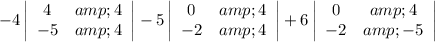
To find the determinants of the 2x2 matrices, multiply the top left and bottom right, then subtract the top right times the bottom left.
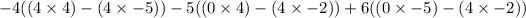
Simplify: