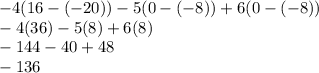Question

Hiya! can anyone help me with these? it would be greatly appreciated!

Answer 1

k = -6

w = ±9

f = -7

Determinant = -136

Explanation:

`\left[\begin{array}{cc}-12&-w^(2)\\2f&3\end{array}\right] =\left[\begin{array}{cc}2k&-81\\-14&3\end{array}\right]`

Each cell in the left matrix equals the corresponding cell in the right matrix:

-12 = 2k → k = -6

-w² = -81 → w = ±9

2f = -14 → f = -7

`\left|\begin{array}{ccc}-4&5&6\\0&4&4\\-2&-5&4\end{array}\right|`

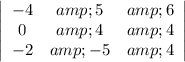
To find the determinant of a 3x3 matrix, you can use something called "Laplace expansion".

Start with the first column in the top row (-4). If you block out the row and column containing that cell, you get a 2x2 matrix:

`\left|\begin{array}{ccc}*&*&*\\ *&4&4\\ *&-5&4\end{array}\right|`

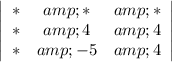
Multiply the -4 by the determinant of that 2x2 matrix:

`-4\left|\begin{array}{cc}4&4\\-5&4\end{array}\right|`

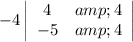
Repeat for the other two cells in the top row.

`5\left|\begin{array}{cc}0&4\\-2&4\end{array}\right|`

`6\left|\begin{array}{cc}0&4\\-2&-5\end{array}\right|`

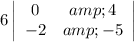
Add them together, alternating the signs (first column positive, second column negative, third column positive).

`-4\left|\begin{array}{cc}4&4\\-5&4\end{array}\right|-5\left|\begin{array}{cc}0&4\\-2&4\end{array}\right|+6\left|\begin{array}{cc}0&4\\-2&-5\end{array}\right|`

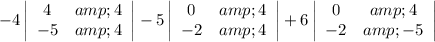
To find the determinants of the 2x2 matrices, multiply the top left and bottom right, then subtract the top right times the bottom left.
`-4((4*4)-(4*-5))-5((0*4)-(4*-2))+6((0*-5)-(4*-2))`

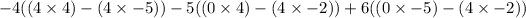
Simplify:

`-4(16-(-20))-5(0-(-8))+6(0-(-8))\\-4(36)-5(8)+6(8)\\-144-40+48\\-136`

Answer 2

K would be -6 and w would be 9