Question

A race car rounds one end of a speedway. This end of the track is a turn with a radius ???? of approximately 187 ft. If the track is assumed to be completely flat and the race car is traveling at a constant 74.00 mi/h around the turn, what is the race car's centripetal (radial) acceleration ????c? ????c= 63.0 ft/s2 Convert this result to SI units. ????c= 19.2 m/s2 What is the force responsible for the centripetal acceleration in this case?\

Answer 1

Friction between the tires and the track.

Step-by-step explanation:

The formula for radial (centripetal) acceleration is:

`a_(cp)=(v^2)/(r)`

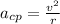
We want our result in
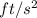`ft/s^2`, so we need to transform the units of v and r to those units. r are already on ft, and for v we use conversion factors. Since there are 5280 feet in a mile, if we divide one by the other we get the number 1, and since there are 3600 second in an hour, if we divide one by the other we also get the number 1, so we can multiply them by any magnitude to change just the units, without changing the actual magnitude (again, since these factors are equal to 1):

`v=74.00\ mi/h=74(mi)/(h) ((5280\ feet)/(1\ mi)) ((1\ h)/(3600\ s))=108.53 ft/s`

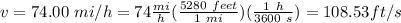
And use our formula:

`a_(cp)=(v^2)/(r)=((108.53ft/s)^2)/(187ft)=63.0ft/s^2`

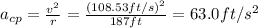
To convert to S.I. we remember that 1 ft is 0.3048 m:

`a_(cp)=63.0ft/s^2=63.0(ft)/(s^2) ((0.3048m)/(1ft))=19.2m/s^2`

The force responsible for the centripetal acceleration is provided by the friction between the tires and the track.