Question

A town has 5000 people in year t = 0. Calculate how long it takes for the population P to double once, twice, and three times, assuming that the town grows at a constant rate of (a) 500 people per year. double once t = 10 Correct: Your answer is correct. years double twice t = 30 Correct: Your answer is correct. years double three times t = 70 Correct: Your answer is correct. years (b) 5% per year. (Round your answer to three decimal places.) double once t = 14.207 Correct: Your answer is correct. years double twice t = 28.413 Correct: Your answer is correct. years double three times t = 42.620 Correct: Your answer is correct. years

Answer 1

Explanation:

At the time t = 0, population of the town = 5000

Rate of population increase = 500 per year

Therefore, the equation that will represent the population will be

`P_(t)=P_(0)+500t`

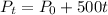
Where
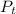`P_(t)` = Population after t years

`P_(0)`= Initial population

t = Time in years

a). For double once the population will be 500×2 = 10000

By plugging in the values in the equation,

10000 = 5000 + 500t

500t = 10000 - 5000

500t = 5000

t =
`(5000)/(500)`

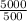
t = 10 years

For Double twice,

Population will be = 10000×2 = 20000

Now we plug in the values in the equation again

20000 = 5000 + 500t

500t = 20000 - 5000

500t = 15000

t =
`(15000)/(500)`

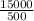
t = 30 years

For double thrice,

Population of the town = 20000×2 = 40000

Now we plug in the values in the equation,

40000 = 5000 + 500t

500t = 40000 - 5000

500t = 35000

t =
`(35000)/(500)`

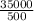
t = 70 years

b). If the population growth is 5%.

Then the growth will be exponential represented by

`T_(n)=T_(0)(1+(r)/(100))^(t)`

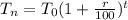
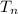`T_(n)` = Population after t years

`T_(0)` = Initial population

t = time in years

For double once,

Population after t years = 10000

`10000=5000(1+(5)/(100))^(t)`

`(1.05)^(t)=(10000)/(5000)`

`(1.05)^(t)=2`

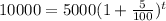
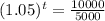
Take log on both the sides

`log(1.05)^(t)=log2`

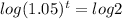
tlog(1.05) = log2

t =
`(log2)/(log1.05)`

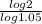
t = 14.20 years

For double twice,

Population after t years = 20000

`20000=5000(1+(5)/(100))^(t)`

`(1.05)^(t)=(20000)/(5000)`

`(1.05)^(t)=4`

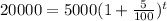
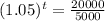
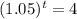
Take log on both the sides

`log(1.05)^(t)=log4`

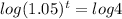
tlog(1.05) = log4

t =
`(log4)/(log1.05)`

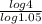
t = 28.413 years

For double thrice

Population after t years = 40000

`40000=5000(1+(5)/(100))^(t)`

`(1.05)^(t)=(40000)/(5000)`

`(1.05)^(t)=8`

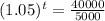
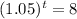
Take log on both the sides

`log(1.05)^(t)=log8`

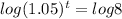
tlog(1.05) = log8

t =
`(log8)/(log1.05)`

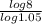
t = 42.620 years