Question

The web logs of a certain website show that the average number of hits in an hour is 75 with a standard deviation equal to 8.6. We can assume that the number of hits in an hour is normally distributed. a) What’s the probability of observing less than 60 hits in an hour? Use the normal approximation. b) What’s the 99th percentile of the distribution of the number of hits? Use the normal approximation. c) What’s the probability of observing between 80 and 90 hits an hour? Use the normal approximation.

Answer 1

a) There is a 10.75% probability of observing less than 60 hits in an hour.

b) The 99th percentile of the distribution of the number of hits is 95.21 hits.

c) There is a 24% probability of observing between 80 and 90 hits an hour

Explanation:

Problems of normally distributed samples can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by

`Z = (X - \mu)/(\sigma)`

After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X. The sum of the probabilities is decimal 1. So 1-pvalue is the probability that the value of the measure is larger than X.

In this problem, we have that

The web logs of a certain website show that the average number of hits in an hour is 75 with a standard deviation equal to 8.6, so
`\mu = 75, \sigma = 8.6`.

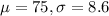a) What’s the probability of observing less than 60 hits in an hour? Use the normal approximation

This is the pvalue of Z when X = 60. So

`Z = (X - \mu)/(\sigma)`

`Z = (60 - 75)/(8.6)`

`Z = -1.74`

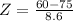
`Z = -1.74` has a pvalue of 0.1075. This means that there is a 10.75% probability of observing less than 60 hits in an hour.

b) What’s the 99th percentile of the distribution of the number of hits?

What is the value of X when Z has a pvalue of 0.99.

Z = 2.35 has a pvalue of 0.99

So

`Z = (X - \mu)/(\sigma)`

`2.35 = (X - 75)/(8.6)`

`X - 75 = 20.21`

`X = 95.21`

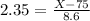
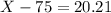
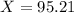
The 99th percentile of the distribution of the number of hits is 95.21 hits.

c) What’s the probability of observing between 80 and 90 hits an hour?

This is the pvalue of the zscore of X = 90 subtracted by the pvalue of the zscore of X = 80.

For X = 90

`Z = (X - \mu)/(\sigma)`

`Z = (90 - 75)/(8.6)`

`Z = 1.74`

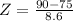
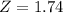
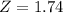`Z = 1.74` has a pvalue of 0.95907

For X = 80

`Z = (X - \mu)/(\sigma)`

`Z = (80 - 75)/(8.6)`

`Z = 0.58`

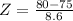
`Z = 0.58` has a pvalue of 0.71904

So

There is a 0.95907 - 0.71904 = 0.24003 = 24% probability of observing between 80 and 90 hits an hour