Answer:
(A). The change in the electron’s kinetic energy is
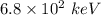 .
.
(B). The distance is 30.95 km.
(C). The direction of electron is opposite direction of the electric field.
Step-by-step explanation:
Given that,
Electric strength
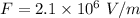
Distance = 0.325 m
(A). We need to calculate the change in the electron’s kinetic energy
Using formula of work done
Kinetic energy=Work done by electric force
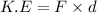
Put the value into the formula

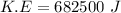
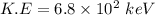
The change in kinetic energy is
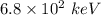 .
.
(B). Given that,
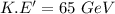
We need to calculate the distance
Using formula of kinetic energy
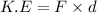
Put the value into the formula
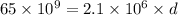
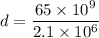

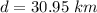
The distance is 30.95 km.
(C). We know that,
The direction of force is taken the direction of electric field.
If the charge is negative then the direction of force is opposite direction of electric field.
So, The direction of electron is opposite direction of the electric field.
Hence, This is the required solution.