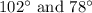Question

Find the measure of two supplementary angles if the diffrence in measure of the two angles is 24

Answer 1

the two angles are 78 and 102 degrees

Explanation:

included in the picture is the explanation. Use simultaneous equation to solve. hope this helps :)

Answer 2

The measure of two supplementary angles are
`102^(\circ) \text { and } 78^(\circ)`

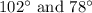
Solution:

Given that the difference of measure of the two angles is 24

Let the first angle be x and the second angle be x-24. We know when two angles are supplementary their sum is equal to
`180^(\circ)`

Now since x and (x-24) are two supplementary angles, therefore their sum will be equal to
`180^(\circ)`

x+(x-24) = 180

2x-24=180

2x= 180+24

2x = 204

`x = (204)/(2)`

`\mathrm{x}=102^(\circ)`

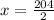
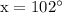
The first angle is
`102^(\circ)`

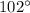
The second angle is (x – 24) so we get (102 - 24) = 78

Hence the measure of two supplementary angles are
`102^(\circ) \text { and } 78^(\circ)`