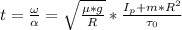Question

A platform is free to rotate in the horizontal plane about a frictionless, vertical axle. About this axle the platform has a moment of inertia Ip. An object is placed on a platform a distance R from the center of the axle. The mass of the object is m and it is very small in size. The coefficient of friction between the object and the platform is μ. If at t = 0 a torque of constant magnitude τ0 about the axle is applied to the platform when will the object start to slip?

Answer 1

It will start to slip at
`t=\sqrt{(\mu*g)/(R)}*(I_p+m*R^2)/(\tau_0)`

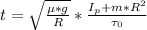
Step-by-step explanation:

We can find the angular acceleration from a sum of torque on the system:

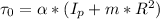`\tau_0=\alpha *(I_p+m*R^2)` Solving for α

`\alpha =(\tau_0)/(I_p+m*R^2)`

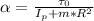
Now, on the object, we make a sum of forces on the centripetal-axis:

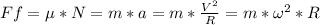`Ff=\mu*N=m*a=m*(V^2)/(R) =m*\omega^2*R` Solving for ω:

`\omega=\sqrt{(\mu*N)/(m*R) }`

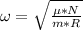
From a sum of forces on the axis perpendicular to the platform:

`N-m*g=0`
`N=m*g`

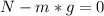
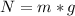
Replacing this value into the ω equation:

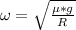`\omega=\sqrt{(\mu*g)/(R) }` Now we have to find the amount of time that takes to the object to get this speed.

`\omega=\alpha *t` Solving for t:

`t=(\omega)/(\alpha) =\sqrt{(\mu*g)/(R)}*(I_p+m*R^2)/(\tau_0)`