Question

4.71 A full-wave rectifier circuit with a 1-kΩ operates from a 120-V (rms) 60-Hz household supply through a 6-to-1 transformer having a center-tapped secondary winding. It uses two silicon diodes that can be modeled to have a 0.7-V drop for all currents. What is the peak voltage of the rectified output? For what fraction of a cycle does each diode conduct? What is the average output voltage? What is the average current in the load?

Answer 1

`V_(p (load)) = 28,3 V - 0,7 V = 27,6 V`

`V_(p (load)) = 27,6 V\\V_(avg) = 17,57 V`

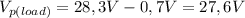
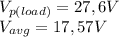
The upper diode conduces in the odd half cycles. The lower diode conduces in the even half cycles.

`I_(avg) = (V_(avg))/(R_(load)) = (17,57 V)/(1000 Ω) = 17,57 mA`

Step-by-step explanation:

The peak voltage after the 6 to 1 step down is
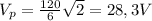`V_(p) = (120)/(6) √(2) =  28,3V`. Then, the peak voltage of the rectified output is
`V_(p) - [tex]V_(avg) = (2V_(p (load)) )/(\pi)  = (55,2 V)/(\pi ) = 17,6 V`V_{d}[/tex] and according to the statement, the diodes can be modeled to be
`V_(d) = 0,7 V`. Then, the peak voltage in the load is
`V_(p (load)) = 28,3 V - 0,7 V = 27,6 V`.

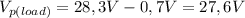The upper diode conduces in the odd half cycles. The lower diode conduces in the even half cycles.

The average output voltage is calculated as:

`V_(p (load)) = 27,6 V\\V_(avg) = 17,57 V`

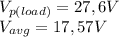
The average current in the load is calculated as:

`I_(avg) = (V_(avg))/(R_(load)) = (17,57 V)/(1000 Ω) = 17,57 mA`