Question

The Machine Shop has received an order to turn three alloy steel cylinders. Starting diameter = 250 mm and length = 625 mm. Feed = 0.30 mm/rev, and depth of cut = 2.5 mm. A coated carbide cutting tool will be used whose Taylor tool life parameters are n = 0.25 and C = 700, where the units are min for tool life and m/min for cutting speed. Compute the cutting speed that will allow the tool life to be just equal to the cutting time for the three parts.

Answer 1

cutting speed is 365.71 m/min

Step-by-step explanation:

given data

diameter D = 250 mm

length L = 625 mm

Feed f = 0.30 mm/rev

depth of cut = 2.5 mm

n = 0.25

C = 700

to find out

the cutting speed that will allow the tool life to be just equal to the cutting time for the three parts

solution

we will apply here cutting time formula that is express as

Tc =
`(\pi DL)/(1000*f*V)` .......................1

here D is diameter and L is length and f is feed and V is speed

so we get

Tc =
`(\pi (250)*625)/(1000*0.3*V)`

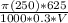
Tc =
`(1636.25)/(V)`

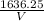
and we know tool life is

T = 3 × Tc ................................2

here T is tool life and Tc is cutting time

so find here tool life by put value in equation 2

T = 3 ×
`(1636.25)/(V)`

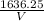
by taylor tool formula cutting speed is

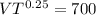
`VT^(0.25) = 700`

V ×
`(3*(1636.25)/(V))^(0.25) = 700`

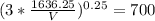
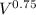`V^(0.75)` × 8.37 = 700

V = 365.71

so cutting speed is 365.71 m/min