Answer:

Explanation:
We are given that

We have to prove that


Therefore, AB=AC
Suppose , angle B and angle C are not congruent.
Then, the measure of one angle is greater than the other.
If
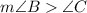
Then ,
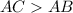
By using triangle parts theorem
It states that when an angle is greater than other then opposite side of greater angle is greater than the opposite side of other angle.
If
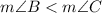
Then, AC < AB.
It is contradiction because we are given AB=AC.
Therefore, it can be concluded that
