Question

A fair coin will be tossed 200,000 times. Let X denote the number of Tails. (a) What is the expected value and the standard deviation of X? (b) Consider a game in which you have to pay $5 in order to earn $log10(X) when X > 0. Is this a fair game? If not, your expected profit is positive or negative?

Answer 1

Answer and explanation:

Given : A fair coin will be tossed 200,000 times. Let X denote the number of Tails.

To find :

(a) What is the expected value and the standard deviation of X?

Given that total number of tosses is n=200000

Probability of getting tail in single toss is p=0.5

Expected value is given by,

`E(X)=n* p`

`E(X)=200000* 0.5`

`E(X)=100000`

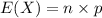
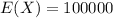
Standard deviation is given by,

`SD=√(n* p* q)`

`SD=√(200000* 0.5* 0.5)`

`SD=√(50000)`

`SD=223.60`

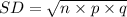
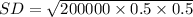
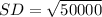
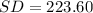
(b) Consider a game in which you have to pay $5 in order to earn
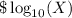`\$\log_(10)(X)` when X > 0. Is this a fair game? If not, your expected profit is positive or negative?

We have to pay $5 to get
`\$\log_(10)(X)`

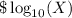
Minimum number of tails required to get $5 is 100000 .

Since, we get X=100000 with Probability 0.5 and for winning we need more number of tosses.

Probability of losing is more than profit hence it's biased test .

As expected number of tails =100000

So profit is given by,

`P=\$\log_(10)(100000)-5`

`P=\$\log_(10)(10^5)-5`

`P=5-5`

`P=0`

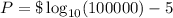
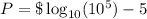
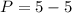
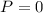
Therefore, The profit is zero.