Question

The highest speed of a cheetah is 100 km/hr and the highest speed of a gazelle is 80 km/hr. If at t = 0 both animals are running at their respective highest speeds, with the gazelle a distance 100 m ahead of the cheetah, at what time does the cheetah catch up with the gazelle? Both the cheetah and the gazelle run in the same direction in a straight line.

Answer 1

t=18s

Step-by-step explanation:

The final position of an object moving at constant speed is given by the formula
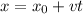`x=x_0+vt`, where
`x_0` is its initial position, v its speed and t the time elapsed.

For the cheetah we have
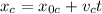`x_c=x_(0c)+v_ct`, and for the gazelle
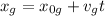`x_g=x_(0g)+v_gt`. We want to know at which t their positions are equal, that is,
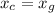`x_c=x_g`, which means,

`x_(0c)+v_ct=x_(0g)+v_gt`

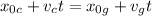
Where we can do:

`v_ct-v_gt=x_(0g)-x_(0c)`

`(v_c-v_g)t=x_(0g)-x_(0c)`

`t=(x_(0g)-x_(0c))/(v_c-v_g)`

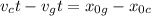
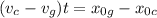
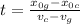
We then substitute the values we have (the initial position of the cheetah is 0m), writing the meters in km so distance units cancel out correctly:

`t=(0.1km-0km)/(100km/hr-80km/hr)=0.005hr=18s`

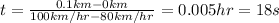
On the last step we just multiply by 3600 because is the number of seconds in an hour.