Question

A car traveling 57.7 km/h is 22.2 m from a barrier when the driver slams on the brakes. The car hits the barrier 2.14 s later. (a) What was the car's constant acceleration just before impact? (Assume the car is initially travelling in the positive direction; if the car decelerates in that direction, its acceleration will be a negative number.)

Answer 1

Step-by-step explanation:

It is given that,

Initial speed of the car, u = 57.7 km/hr = 16.02 m/s

Distance between the car and the barrier, d = 22.2 m

The car hits the barrier 2.14 s later.

Final speed of the car, v = 0 (at rest)

Let a is the acceleration of the car. It can be calculated using the second equation of motion as :

`d=ut+(1)/(2)at^2`

`a=(2(d-ut))/(t^2)`

`a=(2(22.2-16.02* 2.14))/((2.14)^2)`

`a=-5.27\ m/s^2`

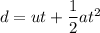
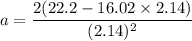
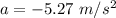
As the car decelerates, the acceleration of the car just before the impact is
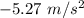`-5.27\ m/s^2`. Hence, this is the required solution.