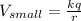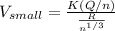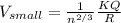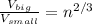Question

A uniformly charged spherical droplet of mercury has electric potential Vbig throughout the droplet. The droplet then breaks into n identical spherical droplets, each of which has electric potential Vsmall throughout its volume. The n small droplets are far enough apart from one another that they do not interact significantly.

Find (Vbig)/(Vsmall) , the ratio of Vbig, the electric potential of the initial drop, to Vsmallthe electric potential of one of the smaller drops.(The ratio should be dimensionless and should depend only on n)

Answer 1

`(V_(big))/(V_(small)) = n^(2/3)`

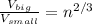
Step-by-step explanation:

Let the total charge on the big drop is given as Q

now if the radius of the drop is R then electric potential of the big drop is given as

`V_(big) = (KQ)/(R)`

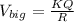
Now if it break into n identical drops

then let the charge on each drop is "q" and radius is "r"

by volume conservation

`(4)/(3)\pi R^3 = n((4)/(3)\pi r^3)`

`r = (R)/(n^(1/3))`

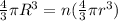
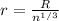
now we have potential of smaller drop given as

`V_(small) = (kq)/(r)`

`V_(small) = (K(Q/n))/((R)/(n^(1/3)))`

`V_(small) = (1)/(n^(2/3))(KQ)/(R)`

`(V_(big))/(V_(small)) = n^(2/3)`