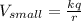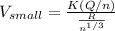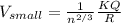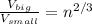Answer:
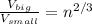
Step-by-step explanation:
Let the total charge on the big drop is given as Q
now if the radius of the drop is R then electric potential of the big drop is given as
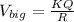
Now if it break into n identical drops
then let the charge on each drop is "q" and radius is "r"
by volume conservation
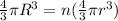
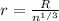
now we have potential of smaller drop given as