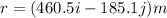Question

A fish swimming in a horizontal plane has velocity i = (4.00 î + 1.00 ĵ) m/s at a point in the ocean where the position relative to a certain rock is i = (12.0 î − 3.60 ĵ) m. After the fish swims with constant acceleration for 15.0 s, its velocity is = (15.0 î − 6.00 ĵ) m/s.

Answer 1

Question is missing. Found on google:

a) What are the components of the acceleration of the fish?

(b) What is the direction of its acceleration with respect to unit vector î?

(c) If the fish maintains constant acceleration, where is it at t = 30.0 s?

(a)
`(0.73, -0.47) m/s^2`

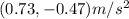
The initial velocity of the fish is

`u=(4.00 i + 1.00 j) m/s`

while the final velocity is

`v=(15.0 i - 6.00 j) m/s`

Initial and final velocity are related by the following suvat equation:

`v=u+at`

where

a is the acceleration

t is the time

The time in this case is t = 15.0 s, so we can use the previous equation to find the acceleration, separating the components:

`v_x = u_x + a_x t\\a_x = (v_x-u_x)/(t)=(15.0-4.00)/(15.0)=0.73 m/s^2`

`v_y = u_y + a_y t\\a_y = (v_y-u_y)/(t)=(-6.00-1.00)/(15.0)=-0.47 m/s^2`

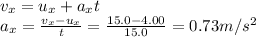
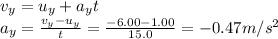
(b)
`-32.8^(\circ)`

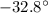
The direction of the acceleration vector with respect to i can be found by using the formula

`\theta = tan^(-1)((a_y)/(a_x))`

where

`a_x` is the horizontal component of the acceleration

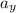`a_y` is the vertical component of the acceleration

From part a), we have

`a_x = 0.73 m/s^2`

`a_y = -0.47 m/s^2`

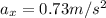
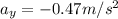
Substituting,

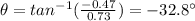
`\theta = tan^(-1)((-0.47)/(0.73))=-32.8^(\circ)`

(c)
`r=(460.5 i - 185.1 j )m`

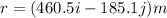
The initial position of the fish is

`r_0 = (12.0 i -3.60 j) m`

The generic position r at time t is given by

`r= r_0 + ut + (1)/(2)at^2`

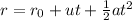
where

`u=(4.00 i + 1.00 j) m/s` is the initial velocity

`a=(0.73 i -0.47 j) m/s^2` is the acceleration

Substituting t = 30.0 s, we find the final position of the fish. Separating each component:

`r_x =12.0 + (4.00)(30) + (1)/(2)(0.73)(30)^2=460.5 m\\r_y = -3.60 + (1.00)(30) + (1)/(2)(-0.47)(30)^2=-185.1 m`

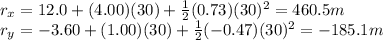
So the final position is

`r=(460.5 i - 185.1 j )m`